Region Simplification
These methods can be used to simplify regions as a preprocessing step
before they are fed to labeled region scanning methods.
Halfplane Compression
These methods provide guarantees on regions with respect to halfplanes.
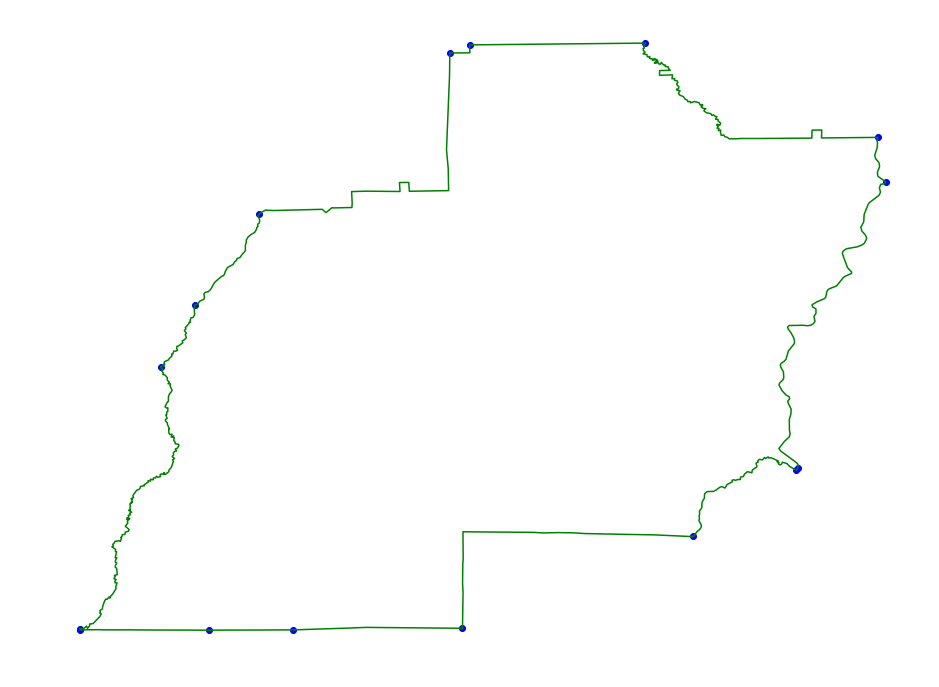
Convex Hull
This method takes the convex hull of the trajectory. Since points
internal to the convex hull will not effect halfplane labeled scanning
we can do this as a preprocessing step to speed up the scanning without
effecting the spatial error.
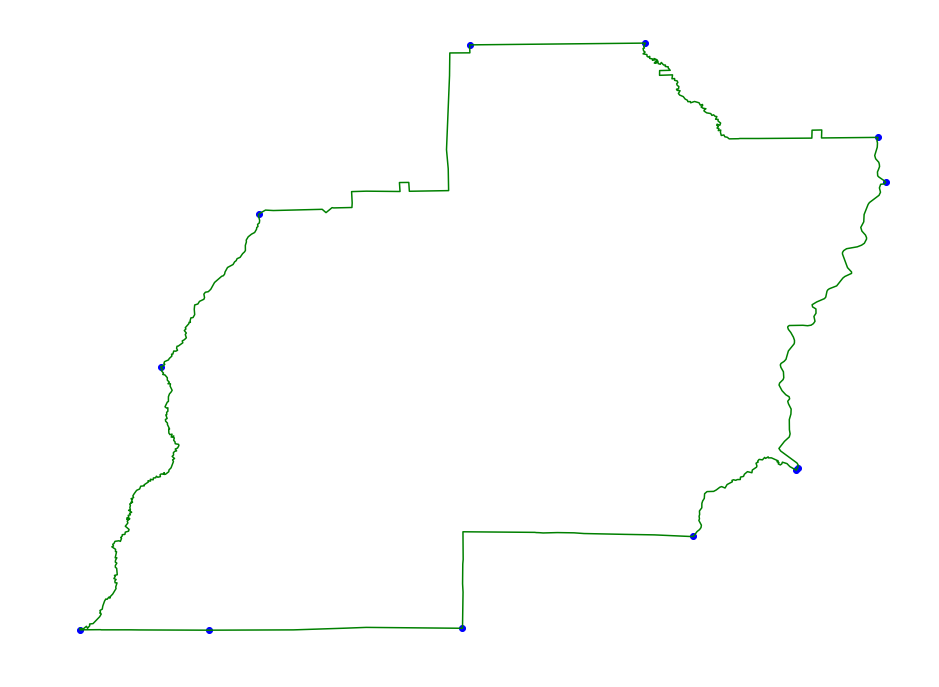
Directional Hull
This method uses an approximation of the convex hull to simplify the
region even more. The spatial error is bounded by alpha. In practice
this method can reduce the number of points needed significantly over
just taking the convex hull, and therefore speed up halplane labeled
scanning even more than the previous method.
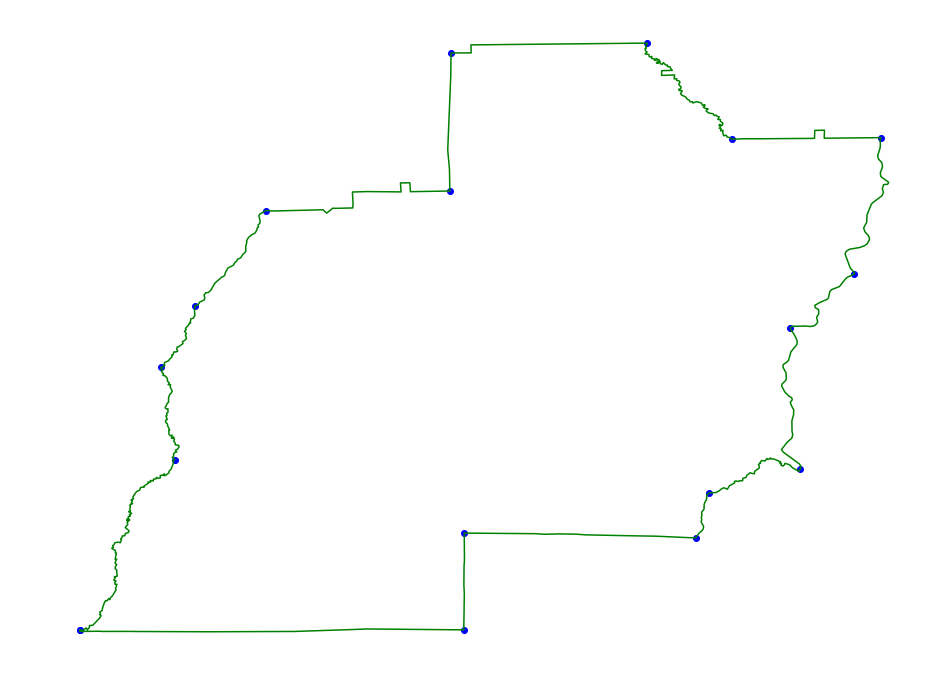
DP Simplification
This is the popular Douglas Peucker simplification algorithm. It has the
same error guarantees as the Directional Hull method, but usually
produces a larger number of points per region.
Disk(or Rectangle) Compression
For disk or rectangle regions we have to handle the inside of the
region. We need a guarantee that any disk or rectangle of a certain
minimum size contained completely inside the region will be hit. We then
handle the boundaries of the region differently then the insides to get
the correct guarantees for certain regions.
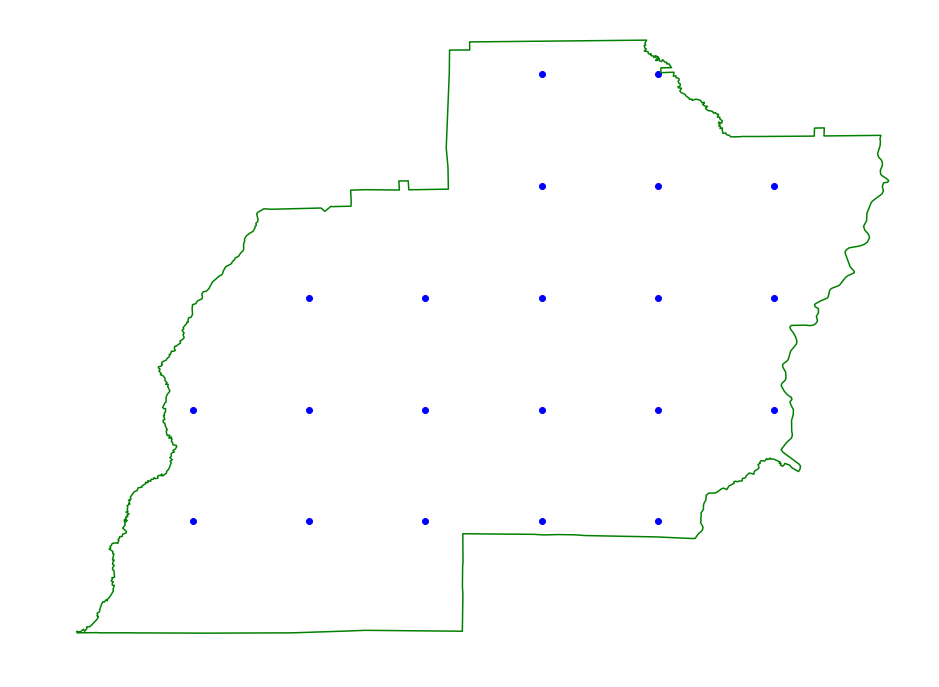
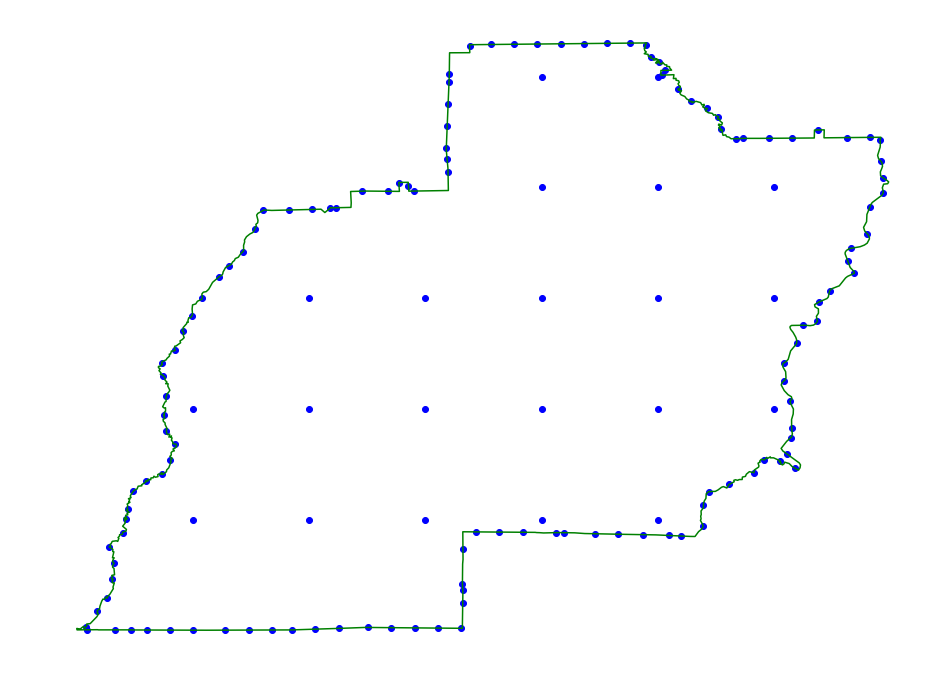
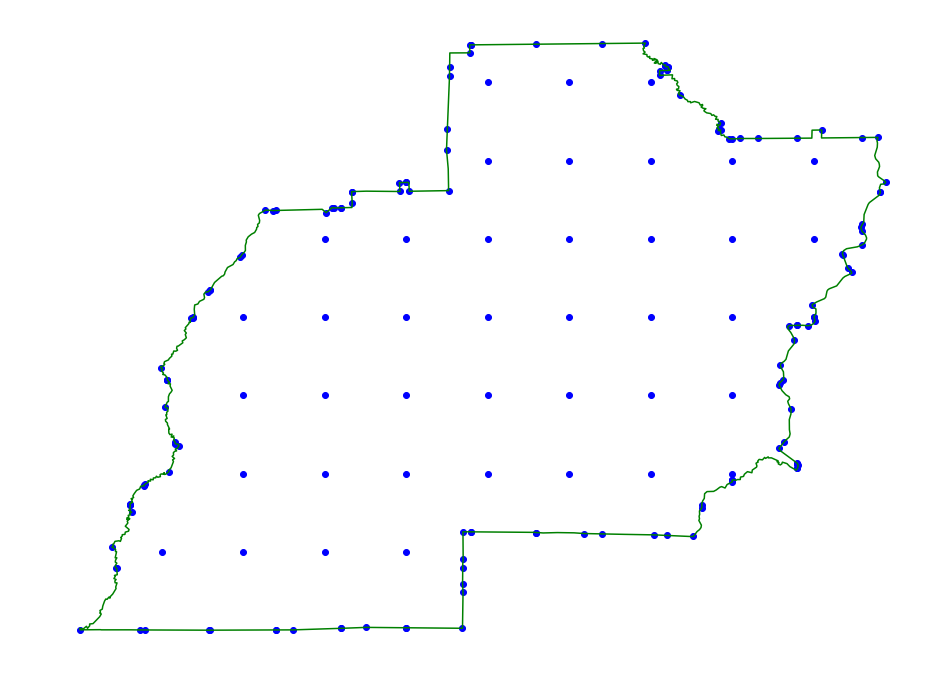
Gridding
We can apply a grid inside of the region.
Boundary Conditions
Below we show a couple of different boundary methods. We recommend using
the grid even for rectangles and grid_hull version for disks. Even
chooses points at even spaced intervals along the region boundary. Grid
hull grids the boundary of the region using a different resolutions
based on the \(\alpha\) parameter and then applies a directional
hull aproximation internally. The r_min parameter is the minimum radius
of the disk that we get \(\alpha\) error on.
 pyscan
1.0
pyscan
1.0